How do you calculate the Stochastic projection graphs?

The stochastic projection graphs use a fund’s historic returns to estimate the probability of future returns. Synaptic Research runs 10,000 Monte Carlo projections per fund and then shows every fifth percentile return between the 5^th and 95^th percentiles. The median estimated return is highlighted using a diamond shape.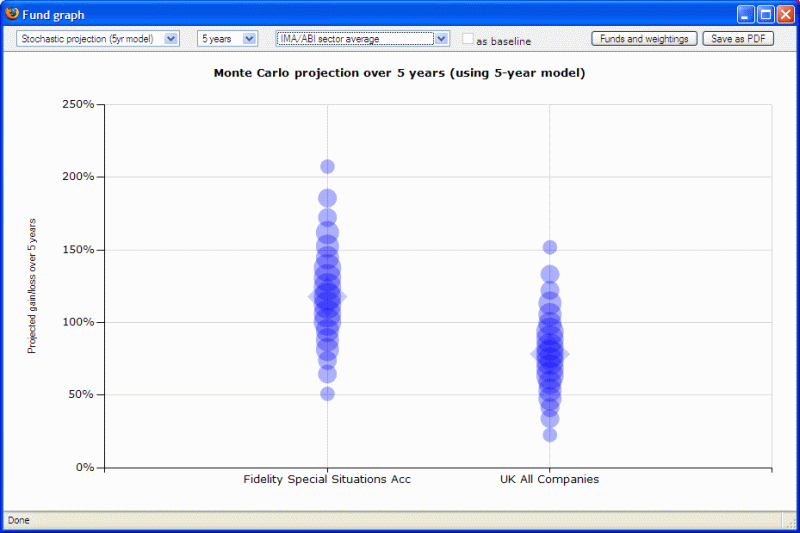

In the first example screenshot above, Synaptic Research is estimating the median of the fund’s projected returns over 5 years to be a gain of about 120% - there is a 50% chance that returns will exceed this, and equally a 50% chance that returns will fall below this level. The 5^th percentile is a gain of 50% - i.e. Synaptic Research is estimating a probability of 5% that the fund will gain less than 50% over 5 years (and therefore that the probability of the fund losing money is very low indeed). The graph has also been configured to show the same projection for the sector average: a tighter spread of projected returns; a much lower median return; and more chance of losing money.

The Monte Carlo projections use actual historic returns over either the last 5 or 10 years, depending on which version of the graph that you use. (Funds cannot be graphed unless they have at least 5/10 years of returns.) The 10-year model will often produce different estimates than the 5-year model. The second example graph below is looking at the same funds and time period as the above example, but is producing lower estimates.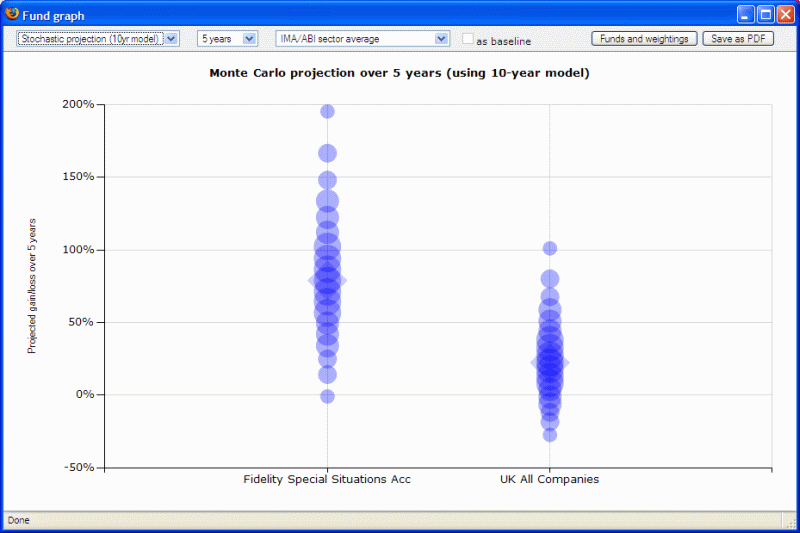

This is because the returns on funds during the period 5 to 10 years ago will be different to the returns during the most recent 5 years. Where the most recent 5 years have seen better performance than years 6-10, the 10 year graph will tend to be more pessimistic than projections based on only 5 years of data (and vice-versa).It’s up to users to decide which they consider 5 years or 10 years to be more realistic. As with all such stochastic models, there are various assumptions implicit in the projection: past performance is (in a sense) a guide to future performance; things which haven’t happened in the past won’t happen in future; and all historic returns are independent and do not affect each other (and therefore funds do not exhibit any form whatsoever of mean reversion).